11-08-2006 | KHOA HỌC

Con Số 5

  GS.NGUYỄN XUÂN VINH và GS. NGUYỄN PHÚ THỨ

Giáo sư Nguyễn Xuân Vinh và Giáo sư Nguyễn Phú Thứ, một người ở Hoa Kỳ và một người ở Pháp, nhưng có cùng một tâm niệm là góp chung những kiến thức của mình để viết bằng tiếng Việt những bài luận thuyết về khoa học thường thức và phổ biến tới đại chúng. Lần này hai ông viết về những kỳ diệu của con số 5.

Phàm người đời thường cho rằng, tất cả hiện hữu có được trên quả đất này từ con người đến thú vật cũng như cây cỏ và vật dụng … đều có số hết cả! Có nhiều con số đáng cho chúng ta suy ngẫm. Riêng đối vớI con người, khi lọt lòng mẹ sanh ra cũng tính bằng con số, bởi vì, từ khi người mẹ thụ thai đến khi lọt lòng mẹ phải mất một thời gian khoảng 9 tháng 10 ngày, rồi khi ta lớn lên đến khi lìa đời cũng phải mất một thời gian dài hay ngắn, nếu người chết có số tuổi cao xem như chết già tức có số trường thọ; còn trái lại, người đó chết tuổi thấp xem như chết non tức có số chết yểu; hoặc người sanh ra được số sung sướng giàu sang phú quý hay bị số bất hạnh, nghèo khó. Điều đó ta gọi là số mệnh. Vì luận đoán số mệnh đưa vào tuổi thọ, tức là thời gian dài hay ngắn, và tiền của nhiều hay ít hoặc phúc trạch là có đông con cái hay không; nên người ta phải có những con số để đo lường...

Nhận định chung về con số 5 :

Nếu chúng ta xét cho kỹ, thì thấy con số đó chỉ là con số chẵn hoặc con số lẻ đã được các nhà khoa học tìm ra cho chúng ta sử dụng sau này, nhưng nó chỉ đóng khung trong 10 con số căn bản. Đó là: 0, 1, 2, 3, 4, 5, 6, 7, 8 và 9 (bởi vì, số 0 cũng là con số). Từ đó, chúng ta ghép nối để có những con số lớn hơn. Đây là năm con số chẵn 0, 2, 4, 6, 8 và năm con số lẻ 1, 3, 5, 7, 9. Viết đến đây, chúng tôi lại nhớ: Căn cứ theo Hà Đồ Tiên Thiên Bát Quái gồm có 10 con số là: 1, 2, 3, 4, 5, 6, 7, 8, 9 và 10. Nhưng được phân định như sau:

- Năm con số dương = Trời, tức số lẻ như đã dẫn ở trên là: 1, 3, 5, 7, 9. Nếu chúng ta đem cộng tất cả lại thì có kết quả như sau: 1+3+5+7+9 = 25.

- Năm con số âm = Đất, tức số chẵn như đã dẫn ở trên là: 2, 4, 6, 8, 10. Nếu chúng ta đem cộng tất cả lại thì có kết quả như sau: 2+4+6+8+10 = 30.

Nếu chúng ta cộng kết quả của số dương và số âm thì có được như sau: 25 + 30 = 55. Con số này gồm chung cả thiên địa rất công bằng, vì mỗi thiên và mỗI địa đều có 5 lại tương đắc, công bằng với nhau, vì: “Thiên số ngũ, Địa số ngũ, ngũ vị tương đắc nhị các hữu hiệp” (Số trờI có năm số, số đất có năm số, năm ngôi cùng tương đắc mà điều hạp nhau). Ngoài ra, theo Lão Tử đã viết: “Nhứt sanh nhị, nhị sanh tam, tam sanh vạn vật” và theo Kinh Dịch đã viết: “tam thiên, lưỡng địa” (bởi vì, tiên âm hậu dương) tức Trời 3, Đất 2. Từ đó, người đời thường nói: “Trời cao, Đất rộng” hay “Trời tròn, Đất vuông” là thế đó. Nếu chúng ta cộng Trời 3 là dương với Đất 2 là âm thì số thành là 5 và cộng thêm vạn vật 2, sẽ trở thành 7 tức con số tối đa cuả số nguyên tố trong các con số lẻ đầu tiên, kể từ 1, 3, 5, 7 đến 9; bởi vì con số 9 không phải là số nguyên tố, vì nó có thể chia chẵn làm ba lần, với 1, 3 và 9.

Hơn nữa, nếu chúng ta để ý lấy số lẻ của 5 số dương là: 1, 3, 5, 7, 9 đem cộng lại như đã thấy ở trên, có kết quả là 25 và rồi lấy số 25 tức 2 với 5 cộng lại thì cũng có kết quả là 7.

Trong bài này chúng tôi đặc biệt viết về con số 5, vì nó là kết hợp của Trời (3) và Đất (2). Từ ngàn xưa theo các kinh điển, người ta đã có những nhóm gồm 5 phần tử như sau:

- Ngũ quan gồm có: Tai (nhĩ), Mắt (mục), Mũi (tị), Miệng (khẩu), Lưỡi (thiệt);  

- Ngũ phước gồm có: Phú (giàu có), Thọ (sống lâu), Khương ninh (sức khỏe), Đức (đức hạnh), Khảo chung (trọn than sống); 

- Ngũ hành gồm có: Kim, Mộc, Thủy, Hỏa, Thổ; 

- Ngũ cúng gồm có: Hương, Đăng, Trà, Hoa, Quả; 

- Ngũ thường gồm có: Nhân, Nghĩa, Lễ, Trí, Tín; 

- Ngũ giới cấm là 5 điều ngăn cấm của đạo Phật đối với Phật tử là: Sát sanh, Đạo tặc, Tà dâm, Uống rượu, Nói dối. (Nếu chúng ta nhìn kỹ và so sánh Ngũ Thường của Nho Giáo và Ngũ Giới của Phật Giáo thì thấy có sự liên hợp giống nhau, bởi vì: Nhân = Không sát sanh, Nghĩa = Không đạo tặc, Lễ = Không tà dâm, Trí = Không uống rượu và Tín = Không nói dối). 

- Ngũ Quả gồm có các trái cây như: Mãng cầu, Chùm sung, Dừa tươi, Đu đủ, Xoài; v. v…

Ngoài ra, con số 5 là con số kết hợp Trời và Đất, bởi vì tam Thiên, lưỡng Địa và một đặc điểm đáng lưu ý nữa, trong dân gian mình thường tín ngưỡng cứ mỗi tháng có 3 ngày kỵ xuất hành. Đó là, theo câu ca dao:  

Mùng năm, mười bốn, hăm ba; 

Đi chơi cũng lỗ, lọ là đi buôn. 

Nhưng nếu chúng ta bình tâm mà xét theo con số thì có kết quả ba ngày ấy cũng là số 5, bằng chứng là con số 14 thì 1 và 4 cộng lại = 5; con số 23 cũng vậy, tức 2 + 3 = 5. Do vậy, 3 ngày đó đều có số thành là 5; v. v…

Nhiều tổ chức và kiến trúc thời cận đại cũng có căn bản là số 5, chẳng hạn như cơ quan đầu não quân sự lớn nhất thế giới được đặt ở Ngũ Giác Đài.

Nói về quân sự, khi có binh lực thật mạnh, người xưa chia việc chỉ huy ra cho 5 quân là: tả quân, hữu quân, tiền quân, hậu quân và trung quân. Dưới thời nhà Nguyễn, chức vụ võ quan cao cấp nhất là Chánh Võ Nhất Phẩm được gọi là “Ngũ Quân Đô Thống”. Tại Hoa Kỳ, khi được vinh thăng cấp bậc Thống Chế tột bực trong quân đội như Dwight David Eisenhower (1890 – 1969) thì được dùng 5 ngôi sao cho cấp hiệu.

Trong vạn vật, con số 5 cũng luôn luôn được hiện hình như theo luật thiên nhiên của tạo hóa:

- Nhiều loài hoa hồng quý giá, hay cả những hoa thường như hoa dâm bụt, khi nở cũng xòe ra 5 cánh. 

- Ngôi sao bể là một loài thủy tộc cũng có 5 nhánh thay vì 4 nhánh hay 6 nhánh. 

- Một quả khế cũng có 5 khía chìa ra như muốn mời mọc con người tiền sử lần đầu tiên nếm thử mùi vị chua nồng của loại trái cây mới. 

- Con người ta lúc đầu tiên tập đếm cũng chỉ tới số 5, vì dùng đầu ngón tay cũng chỉ tới được 5 ngón. 

- Khi loài người bắt đầu thu nhập những âm hưởng của thiên nhiên, tiếng chim hót thông reo, tiếng gió thoảng bên khe núi và tiếng suối chảy lưng đèo, để đặt ra cung bậc, cũng xếp thành 5 cung là: Cung, Thương, Giốc, Trủy và Vũ. Như tả về tài đánh đàn của Kiều, cụ Nguyễn Du đã viết:

Cung thương làu bậc ngũ âm, 

Nghề riêng ăn đứt hồ cầm một trương. (Truyện Kiều câu 31-32)

. . . . . 

Ở đây còn nhiều loại khác để chỉ con số 5 không thể kể ra hết được. (Độc giả cần tìm hiểu thêm xin tìm đọc quyển thượng từ trang 419 đến trang 423 của tác phẩm “Tìm hiểu Tử Vi Đẩu Số và Địa Lý” của Nguyễn Phú Thứ).

Số 5 trong Hình học

Trong thiên nhiên, những hình có vẻ đẹp tuyệt vời, thường là những hình được nẩy sinh từ nguyên thủy. Những thí dụ ta nhìn thấy hàng ngày là hình tròn trong mặt phẳng và hình cầu trong không gian. Người tiền sử khi ném một hòn đá xuống mặt hồ sẽ thấy những gợn sóng lan ra như những vòng tròn đồng tâm. Mặt trời, mặt trăng trông cũng có hình tròn, nhưng thật ra là những hình cầu tức là hình tròn trong không gian ba chiều. Ngoài hình tròn ra, trong mặt phẳng, những hình nhiều cạnh đều cũng là những hình đặc biệt. Trước hết ta có hình tam giác đều ba cạnh và hình vuông có bốn cạnh đều nhau. Sau đó đến hình năm cạnh đều và hình sáu cạnh đều. Hình năm cạnh hay cũng còn gọi là hình năm góc, hay hình ngũ giác có nhiều tính chất siêu việt hơn là hình sáu cạnh, mà ta cũng còn gọi là hình lục lăng.

Để chứng tỏ tính chất thiên nhiên của hình ngũ giác ta chỉ cần lấy một băng giấy rồi thắt chéo lại thì sẽ có được một hình ngũ giác đều. Muốn gấp giấy thành một hình lục lăng đều thì phảI hoặc là dùng hai băng giấy hay là phảI dùng một kiểu gấp cầu kỳ hơn nữa, và điều này chứng tỏ rằng hình ngũ giác là một hình thiên nhiên tạo thành.

Theo lẽ tự nhiên của số học, ba con số 3, 4 và 5 phảI đi liền vớI nhau. Cũng vì vậy mà mấy ngàn năm trước đây, người ta đã tìm ra hệ thức là “tổng số bình phương của hai số 3 và 4 sẽ cho ta bình phương của số 5” tức là 3² + 4² = 5².  Cũng vì sự suy luận sau 3 và 4 phải tới 5 mà Pythagore đã tìm được định lý rằng: “một tam giác có cạnh tỷ lệ theo những số này phải là một tam giác vuông”.

Ngưòi Ai Cập cách đây ba ngàn năm và hơn 500 năm trước công nguyên, nhà toán và triết gia Hy Lạp là Pythagore đã biết được rằng có ba cố thể mà tất cả các mặt đều là những hình có cạnh bằng nhau, đó là: hình tháp bốn mặt, hình tám mặt (ở hai cố thể này mỗi mặt là những tam giác đều bằng nhau), và hình thứ ba là hình lập phương có sáu mặt, mỗi mặt là những hình vuông bằng nhau.  

Tới thời triết gia Hy Lạp là Plato vào khoảng 428 – 348 trước công nguyên thì chứng minh được rằng chỉ có 5 cố thể có mặt đều nhau. Hai cố thể sau cùng như trong hình vẽ bên đây là cố thể có 20 mặt, mỗi mặt là những hình tam giác đều bằng nhau và cố thể có 12 mặt, mỗi mặt là những hình ngũ giác đều bằng nhau. Ta nhận thấy không những là chỉ có 5 cố thể hình đều, mà những mặt đều lại chỉ có thể là những hình 3 cạnh, 4 cạnh và 5 cạnh đều mà thôi. Năm hình đã tìm được, gọi là 5 cố thể đều của Plato.

Con số vàng

Ba con số đầu tiên là 1, 2 và 3 hay được ngườI Á Đông chú ý đến. Ngoài số 1 là đơn vị, thường cùng để chỉ một ngôi vị chí tôn, người ta hay dùng số 2 để chỉ Đất và số 3 để chỉ Trời . Căn nhà Việt Nam khi xưa thường cất có 3 gian, 2 chái bao gồm có sân hoa ở giữa. Như thế có nghĩa là thuận hòa được cả Trời và Đất. Về kích thước thành hình chữ nhật, người ta thường dùng khuôn khổ cho khung cửa khi xây cất nhà; hay kích thước lá cờ biểu tượng cho quốc gia, theo t ỷ số 3/2, nghĩa là nếu lấy chiều ngang là 2, thì chiều dài phải là 3 đơn vị. Hình chữ nhật mà có cạnh theo tỷ số 3/2 = 1,5 thường được coi như là một hình đẹp mắt.

Sự thực, tỷ số lý tưởng nhất về phương diện mỹ thuật, lại là một số vô tỷ, nghĩa là không bằng tỷ số của hai số nguyên nào. Số này gọi là số vàng, biểu ký bằng mẫu tự Hy Lạp là = 1,618033 … đã được biết đến và được áp dụng trong sự kiến thiết dinh thự cách đây 25 thế kỷ. 

Vào thế kỷ thứ 13, một trong những nhà số học của thờI Trung Cổ này là Leonardo da Pisa (1175 – 1250) và được gọi tên là Fibonacci, theo tiếng Ý có nghĩa là “con trai của ông Bonacci”. Toán học ở thời đạI này thực ra không tạo được nhiều điều đặc biệt để lưu lại hậu thế, nhưng tình cờ Fibonacci lại tìm ra được một liệt số, tức là một dãy số, khá trùng hợp với cấu trúc của tạo vật như sau: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

Kể từ số hạng thứ ba trở đi, mỗi số hạng của liệt số bằng tổng số của hai số hạng đứng trước. Liệt số này hay gặp ở thiên nhiên. Nhiều nhà thảo mộc học đã tìm ra rằng các cây hay nụ hoa nở trên một cành thường nẩy mầm theo liệt số Fibonacci. Muốn dễ hiểu, ta lấy những số Fibonacci 3, 5, 8, 13 sẽ thấy là nhiều giống hoa đã chọn những số này là số các cánh hoa.  

Một thí dụ đặc sắc nhất là sự bố trí các hạt trên mặt hoa hướng dương, còn gọi là hoa quỳ (Tournesol). Những hạt trên mặt hoa được xếp theo những hình xoắn ốc rất đặc biệt trong toán học gọi là những hình xoắn ốc Logarit. Có những đường xoắn theo chiều kim đồng hồ và những đường xoắn theo chiều ngược lại. Ðiều kỳ lạ là số đường xoắn thuận và số đường xoắn nghịch không bằng nhau mà lạI theo như liệt số Fibonacci. Chẳng hạn hoa nhỏ có 13 đường xoắn theo chiều thuận và 21 đường xoắn theo chiều nghịch. Hoa lớn có thể theo những số (34, 55) và người ta cũng đã tìm được những hoa thật lớn có số vòng thuận và nghịch theo liệt số Fibonacci (89, 144).

Một sự trùng hợp tự nhiên nữa là nếu ta chọn ba số liên tiếp trong liệt số Fibonacci rồi lấy tích số của hai số đầu và cuối rồI trừ đi bình phương của số ở giữa thì sẽ được +1 hay –1. Thí dụ trong liệt số trên, ta thấy: 

2.5 – 3.3 = 1 

3.8 – 5.5 = -1 

5.13 – 8.8 = 1 

8.21 – 13.13 = -1 

13.24 – 21.21 = 1 

Điều huyền diệu nhất ở trong liệt số Fibonacci là nếu gọi Fn là một số hạng trong liệt số thì tỷ số hai số hạng liên tiếp, tức tỷ số Fn +1 và Fn sẽ dẫn đến một số Phi, là một số đặc biệt mà các nhà toán học qua các thời đại đã đồng ý đặt tên là số vàng. Theo liệt số ở trên ta tính được những tỷ số sau đây: 

3/2 = 1.500000       3/5 = 1.666667 

8/5 = 1.600000      13/8 = 1.625000 

21/13 = 1.615385 34/21 = 1.619048 

55/34 = 1.617647   89/55 = 1.618182 

144/89 = 1.617978 233/144 = 1.618056 

= 1.618033989 … 

Cứ tiếp tục mà tính ta sẽ thấy cột bên trái tỷ số tăng dần và tỷ số bên phải giảm dần để cùng hội tụ tại một số Phi gọi là số vàng. Vậy số vàng ở đâu mà ra, và tại sao lại được trân quý như vậy? 

Muốn có một ý niệm khái quát thì chúng ta nhìn hình vẽ của một hình ngũ giác đều trong đó có chứa nhiều hình tam giác cân. Những hình tam giác này được gọi là những tam giác vàng, vì chúng có đặc tính là tỷ lệ của cạnh bên chia cho cạnh đáy thì đúng là số vàng. Hơn nữa, tam giác vàng lại có tính chất hóa sinh rất đặc biệt, từ nó nảy ra nhiều tam giác vàng liên tiếp một cách vô tận. Tính chất này và sự liên hệ giữa hình ngũ giác đều và số vàng sẽ được trình bày dướI đây.

Hình chữ nhật vàng

Điện Parthenon ở Hy Lạp

Vì con số vàng chỉ là một số, dù là một số vô tỷ, viết ra thì dài bất tận, nên trong hình học nó chỉ dùng để biểu thị một tỷ số. Tỷ số này là một mỹ số nên hay được thấy trong hội họa và kiến trúc. Một thí dụ đặc biệt là điện Parthenon ở Hy Lạp, được kiến trúc 5 thế kỷ trước công nguyên, mặt trước của điện lọt vào đúng khuôn khổ một hình chữ nhật mà tỷ số chiều dài chia cho chiều cao lại đúng bằng số vàng = 1,618 … Những hình chữ nhật theo tỷ số này được gọi là hình chữ nhật vàng.

Một thí dụ khác là những thẻ tín dụng bằng plastic rất phổ thong ở thờI đại này cũng có hình thể gần giống như hình chữ nhật vàng. Nhiều nhà tâm lý học đã làm những cuộc thử nghiệm và thấy rằng hình chữ nhật có cạnh theo tỷ số vàng là một hình được ưa chuộng nhất. Cũng vì thế mà những họa sĩ khi lựa chọn kích thước cho những thẻ tín dụng đã chọn tỷ lệ vào khoảng 1.59, nghĩa là cũng gần bằng tỷ số vàng. 

Ta có thể định nghĩa số vàng biểu thị bằng ký hiệu như là một số mà khi trừ đi 1 rồi lấy số nghịch đảo ta lại được số . Viết thành phương trình, ta có:

= 1 / ( -1)

Khai triển ra, ta được:

² – – 1 = 0 

Đây là một phương trình đại số bậc hai, và khi giải ra để lấy đáp số có trị số dương, ta có ngay:

= (1/2) (1 + 5 ) = 1.618033989 … 

Ta thấy ngay là số được tính từ căn hai của số 5 mà ra. Từ trị số nói trên của số vàng, ta suy ra phép vẽ hình chữ nhật vàng như sau: Lấy AB là cạnh có độ dài 1 đơn vị, AB = 1. Sau đó vẽ hình vuông ABEF. Lấy O là trung điểm của AB.

Theo định lý Pythagore, đoạn OE sẽ có độ dài là OE = OC = 5/2. Nếu thế khi vẽ cho trọn hình chữ nhật ACDF thì hình này có chiều dài là AC = , và chiều ngang là AF = 1.

Tỷ số hai chiều là số , và hình chữ nhật là hình chữ nhật vàng.

Hình chữ nhật vàng, hay còn gọi tắt là hình kim nhật, có một tính chất hóa sinh rất đặc biệt. Theo như hình vẽ nếu từ hình chữ nhật lớn, ta bỏ đi hình vuông ABEF, thì còn lại hình chữ nhật nhỏ BCDE. Hình này có cạnh dài là BE = 1. Trong khi ấy thì cạnh ngắn là BC = – 1. Tỷ số hai cạnh của hình chữ nhật này sẽ là 1/( -1) và theo định nghĩa của số vàng thì tỷ số này cũng là số . Vậy thì hình chữ nhật nhỏ này cũng là hình kim nhật. 

Muốn nhìn thấy sự hóa sinh kỳ diệu này ta bắt đầu từ một hình kim nhật lớn ở ngoài cùng. Mỗi lần cắt bớt đi một hình vuông lại có hình kim nhật nhỏ hơn. Nếu ở mỗi hình vuông, dùng compa để vẽ những phần tư vòng tròn liên tiếp nhau thì sẽ được một hình xoắn ốc, gọi là hình xoắn ốc Logarit.

Trong tất cả những hình được goi chung là hình xoắn ốc, thì hình xoắn ốc Logarit có đặc tính là dù ở gần tâm điểm hay vòng ra ngoài xa , hình dạng vẫn giữ nguyên. Tâm điểm này là điểm O, điểm gặp nhau của những đường chéo góc của các hình kim nhật. Trên đường xoắn ốc Logarit, nếu ta lấy một điểm M bất kỳ nào và vẽ bán kính OM và tiếp tuyến MT vớI đường xoắn ốc, thì góc 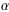(alpha) giữa OM và MT lúc nào cũng giữ nguyên một trị số.

Hình Tam giác vàng 

Trở lại với hình ngũ giác đều theo như hình vẽ ở bên. Nếu vẽ những đường chéo nối những đỉnh của hình ngũ giác đều thì ta sẽ được một ngôi sao năm cánh đều. Những đường chéo hợp với những cạnh của hình ngũ giác thành những tam giác cân có góc ở đỉnh là 36^o và hai góc bằng nhau ở đáy mỗi góc là 72^o, tức là bằng hai lần góc ở đỉnh.

Ở phía trong hình ngôi sao lại hiện ra một hình ngũ giác đều và hình này lại sinh ra một hình ngôi sao 5 cánh đều thứ hai và cứ thế tiếp tục đi vô tận.

Trước công nguyên 5 thế kỷ, trường phái Pythagore đã biết được rằng tỷ số giữa các cạnh của ngôi sao năm cánh và cạnh của hình ngũ giác là số vàng. Đồng thời họ đã biết dùng thước kẻ thẳng và compa để chia tỷ số vàng, nghĩa là họ biết cách để vẽ hình ngũ giác đều, nhưng lại giữ kín không cho người ngoài được biết.

Tất cả những tam giác cân mà ta đã vẽ lồng trong hình ngũ giác đều là những tam giác mà tỷ số cạnh bên chia cho đáy là tỷ số vàng. Ta gọi những tam giác này là tam giác vàng. Tam giác này cũng có tính chất hóa sinh, vì nếu góc ở đáy bằng hai lần góc ở đỉnh, thì khi ta vẽ đường phân giác ở đáy ta lại tạo ra một tam giác vàng khác có góc ở đỉnh bằng 36^o và hai góc đều nhau ở chân mỗi góc bằng 72^o. Ta cũng nhận thấy nếu góc ở đỉnh của một hình lục lăng đều là 120^o thì góc ở đỉnh của một hình ngũ giác đều là 108^o.

Trong văn học Trung Hoa những con số 36, 72 và 108 là những con số được ưa chuộng như là những con số tự nhiên đã có sẵn trong trời đất. Người lớn xem những con số đó như là những số ưu việt, nghĩa là nếu được thêm vào thì coi như là thừa và nếu bớt đi thì lại thấy thiếu sót.

Cũng như vậy trong sách có câu: “Tam thập lục kế tẩu vi thượng sách”  nghĩa là trong ba mươi sáu phương cách thì chạy đi là hơn cả. Cụ Nguyễn Du cũng dùng câu này để tả lời nói của Sở Khanh khi rủ Kiều đi trốn: 

"Thừa cơ lẩn bước ra đi, 

Ba mươi sáu chước, chước gì là hơn?" 

Trong những truyện kiếm hiệp, nhà văn Kim Dung cũng nói là phái Thiếu Lâm có tất cả bảy mươi hai tuyệt kỹ, tức là coi con số này như là một số viên mãn. Trong truyện Thủy Hử cũng chỉ nói tới 108 vị anh hùng trên Lương Sơn Bạc, chứ không thêm vào nữa cho trọn số 120 vị hảo hán. 

Ta cũng có thể bắt đầu từ một tam giác vàng lớn và dùng tính chất hóa sinh để tạo ra nhiều tam giác vàng khác. Như trên hình vẽ, nếu ta vẽ đường phân giác của một góc ở đáy, ta sẽ tạo ra một tam giác vàng nhỏ vì có góc ở đỉnh là 36^o và một góc ở đáy đã là 72^o, thì góc thứ ba cũng sẽ là 72^o và tam giác là tam giác vàng.

Nếu dùng những tam giác được cắt bỏ đi mà vẽ những vòng cung như ở trên hình và nối tiếp những vòng cung lại vớI nhau thì ta lại kiến tạo được một hình xoắn ốc Logarit.

Nguyễn Xuân Vinh & Nguyễn Phú Thứ

Vào Thu hải ngoại, Năm Quý Mùi, 2003

Trích Tuần Báo: Ðời Magazine số 26 ngày 25-10-2003, trang 45.

Cùng Tác Giả:

- Phong Tục Tết Việt Nam Nguyễn Phú Thứ Tiểu luận

- Con số 5 Nguyễn Phú Thứ Khảo cứu