|
|
|
|
|
VĂN HỌC |
GIAI THOẠI | TIỂU LUÂN | THƠ | TRUYỆN | THỜI LUẬN | NHÂN VẬT | ÂM NHẠC | HỘI HỌA | KHOA HỌC | GIẢI TRÍ | TIỂU SỬ |
-
Link Tác Phẩm và Tác Giả Tác Phẩm
Tác Giả
Thơ Văn Trần Yên Hoà & Bằng hữu
Tạp Chí
PHONG HÓA & NGÀY NAY
(Đại học Hoa Sen)
TỰ LỰC VĂN ĐOÀN, tác phẩm
(Viện Việt Học)
VĂN HỌC
Tạp chí Văn Học
DÒNG VIỆT
Trọn bộ DÒNG VIỆT
(1993-2009)
VĂN (Xuân Canh Thìn)
(vanmagazine)
TIỂU THUYẾT THỨ BẢY
NAM PHONG - TRI TÂN
THANH NGHỊ - NGÀY NAY
VĂN HOÁ NGÀY NAY
TẬP SAN SỬ ĐỊA
THẾ KỶ 21 - BÁCH KHOA
Tạp Chí VHNT Miền Nam
TÂN VĂN
TIN VĂN
Tạp chí ĐỌC VÀ VIẾT
THƯ QUÁN BẢN THẢO
Sách Xưa
• QUỐC VĂN GIÁO KHOA THƯ:
- Lớp Sơ Đẳng
- Lớp Đồng Ấu
- Lớp Dự Bị
• TỦ SÁCH TIẾNG VIỆT
• KHO SÁCH XƯA
• QUÁN VEN ĐƯỜNG
• LITTLE SAIGON
Phim và Hình Ảnh Xưa
- Cuộc Di Cư Năm 1954
- Phim "Chúng Tôi Muốn Sống"
- Phim "Nắng Chiều", 1973
- Phim Chân Trời Tím, 1971
- Hình ảnh xưa
eBooks
-
Giải Bài Tập Hình Học từ 41 đến 47 (Học Xá) Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
22-5-2011 | KHOA HỌC
Giải Bài Tập Hình Học từ 41 đến 47
T. V. PHÊ & NGUYỄN TIN
Share File.php Share File




:: Bài 41
P là điểm bất kỳ trên đường cao CD của
 ABC. AP và BP gặp CB và CA lần lươt tại Q và R. Chứng minh rằng
ABC. AP và BP gặp CB và CA lần lươt tại Q và R. Chứng minh rằng  QDC =
QDC =  RDC.
RDC.
(P is any point on altitude CD of
 ABC. AP and BP meet sides CB and CA at points Q and R, respectively. Prove that
ABC. AP and BP meet sides CB and CA at points Q and R, respectively. Prove that  QDC =
QDC =  RDC. (Challenging Problems in Geometry, Alfred S. Posamentier & Charles T. Salkind))
RDC. (Challenging Problems in Geometry, Alfred S. Posamentier & Charles T. Salkind))
BÀI GIẢI
 Đường thẳng // với AB vẽ từ C, cắt DR tại M và DQ tại N.
Đường thẳng // với AB vẽ từ C, cắt DR tại M và DQ tại N.
 RMC ~
RMC ~  RDA ==> MC/AD = RC/RA
RDA ==> MC/AD = RC/RA
==> MC = (AD.RC) / RA.
 QNC ~
QNC ~  QDB ==> NC/DB = QC/QB
QDB ==> NC/DB = QC/QB
==> NC = (DB.QC) / QB.
Lập tỷ số: MC/NC = (AD.RC.QB) / (DB.QC.RA).
Theo định lý Ceva trong tam giác ABC ta có:
(AD/DB).(BQ/QC).(CR/RA) = 1.
Vậy MC/NC = 1. Chứng tỏ MC = NC
==>
 MDN cân, suy ra:
MDN cân, suy ra:  QDC =
QDC =  RDC.
RDC.
Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
:: Bài 42
Cho tam giác ABC nội tiếp trong vòng (O) với đường kính AD.Tiếp tuyến tại D cắt BC tại E. Đường thẳng đi qua E và O cắt hai cạnh AB, AC Tại P, Q theo thứ tự. Chứng minh: OP = OQ.
(Let be given a triangle ABC and AD the diameter of it's circumcircle (O). The tangent line at D of (O) intersect BC at E. Let P = EO
AB, Q = EO
AC. Prove that OP = OQ.
(http://www.mathlinks.ro/viewtopic.php?search_id=1340012344&t=158830))
BÀI GIẢI
 Qua B vẽ đường song song với PQ cắt AC tại F.
Qua B vẽ đường song song với PQ cắt AC tại F.
Gọi M là trung điểm của BC ==> OM
 BC, OD
BC, OD  DE (giả thiết), vậy tứ giác OMDE nội tiếp ==>
DE (giả thiết), vậy tứ giác OMDE nội tiếp ==>  MEO =
MEO =  MDO.
MDO.
Vì PQ//BF ==>
 MEO =
MEO =  MBN, nên
MBN, nên  MBN =
MBN =  MDO (N là giao điểm của AD và BF), vậy tứ giác BMND cũng nội tiếp.
MDO (N là giao điểm của AD và BF), vậy tứ giác BMND cũng nội tiếp.
Do đó:
 BMN +
BMN +  BDN = 180o.
BDN = 180o.
Ta cũng có:
 BCF +
BCF +  BCA = 180o.
BCA = 180o.
Vì
 BDN =
BDN =  BCA nên
BCA nên  BMN =
BMN =  BCF ==> MN // CF ==> N là trung điểm của BF, suy ra O là trung điểm của PQ, vậy:
OP = OQ.
BCF ==> MN // CF ==> N là trung điểm của BF, suy ra O là trung điểm của PQ, vậy:
OP = OQ.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 43
Tiếp tuyến vẽ từ A gặp vòng tròn tâm O tại B và C. Dây cung BF // ADE. Chứng minh rằng FC cắt DE tại trung điểm.
(From point A, tangents are drawn to circle O, meeting the circle at B and C. Chord BF // secant ADE, as in Fig. Prove that FC bisects DE.(Challenging Problems in Geometry, Alfred S. Posamentier & Charles T. Salkind))
BÀI GIẢI
 Tứ giác BACO có hai góc đối
Tứ giác BACO có hai góc đối  ABO và
ABO và  ACO bù nhau nên nội tiếp trong vòng tròn đường kính AO.
ACO bù nhau nên nội tiếp trong vòng tròn đường kính AO.
Ta có
 BAE = ½ (
BAE = ½ (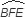 -
- 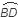 ) = ½ (
) = ½ (
 -
- 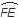 ) = ½
) = ½ 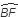 =
=  BCF
BCF
Vậy
 BAM =
BAM =  BCM, chứng tỏ tứ giác BACM cũng nội tiếp trong vòng tròn qua ba điểm B, A, C; đó chính là vòng tròn đường kính AO nêu trên. Suy ra
BCM, chứng tỏ tứ giác BACM cũng nội tiếp trong vòng tròn qua ba điểm B, A, C; đó chính là vòng tròn đường kính AO nêu trên. Suy ra  AMO = 90o.
AMO = 90o.
Trong vòng tròn tâm O, OM
 DE, vậy: DM = EM.
DE, vậy: DM = EM.
Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
:: Bài 44
Cho tiếp tuyến AB tiếp xúc với vòng tròn tại trung điểm M. ACD và BEF là hai cát tuyến. Đường FC cắt AB tại M và đường DE cắt AB tại L. Chứng minh AK = BL.
(The tangent AB touches the circle at M, midpoint of AB. ACD and BEF are two secants. FC meets AB at K and DE meets AB at L. Prove that AK = BL).
BÀI GIẢI
 Ta có phương tích của A và B với vòng tròn:
Ta có phương tích của A và B với vòng tròn:
AM2 = AC . AD, BM2 = BE . BF
Vì AM = BM nên AC . AD = BE . BF (1)
 ADL ==> AL / sin
ADL ==> AL / sin D = AD / sin
D = AD / sin ALD
ALD
 BFK ==> BK / sin
BFK ==> BK / sin F = BF / sin
F = BF / sin BKF
BKF
Thế trị số của AD, BF tính từ các biểu thức trên vào (1), ta có:
AC.(ALsin
 ALD/sin
ALD/sin D) = BE.(BK sin
D) = BE.(BK sin BKF/sin
BKF/sin F) (2)
F) (2)
Vì sin
 D = sin
D = sin F, sin
F, sin ALD = sin
ALD = sin BLE, sin
BLE, sin BKF = sin
BKF = sin AKC
nên (2) có thể viết:
AKC
nên (2) có thể viết: AC.ALsin
 BLE = BE.BKsin
BLE = BE.BKsin AKC hoặc: (AC/sin
AKC hoặc: (AC/sin AKC).AL = (BE/sin
AKC).AL = (BE/sin BLE).BK
BLE).BK
hoặc: (AK/sin
 ACK).AL = (BL/ sin
ACK).AL = (BL/ sin BEL).BK
BEL).BK
==> AK . AL = BL . BK ==> AK2 + AK.KL = BL2 + BL.KL
==> (AK - BL) (AK + BL + KL) = 0 ==> (AK - BL) = 0 ==> AK = BL
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 45
Chứng minh rằng tổng số số đo khoảng cách từ một điểm bên trong tam giác đều đến các cạnh của tam giác ấy là một hằng số.
(Prove that from any point inside an equilateral triangle, the sum of the measures of the distances to the sides of the triangle is constant. (Challenging Problems in Geometry, Alfred S. Posamentier & Charles T. Salkind))
BÀI GIẢI
 Phương pháp I:
Phương pháp I:
Trong tam giác đều ABC, PS
 AC, PR
AC, PR  BC, PQ
BC, PQ  AB và AD
AB và AD  BC.
BC.
Vẽ đường thẳng qua P song song với BC cắt AB, AD, AC lần lượt tại E, G, F. Ta có: PR = GD.
Vẽ ET
 AC. Vì
AC. Vì  AEF đều nên AG = ET.
AEF đều nên AG = ET.
Vẽ PH // AC cắt ET tại N. Ta có: NT = PS (1).
Vì
 EHP đều nên đường cao PQ = EN (2).
EHP đều nên đường cao PQ = EN (2).
Từ (1) và (2) cho ta: PQ + PS = ET = AG.
Vì PR = GD nên PQ + PS + PR = AG + GD = AD.
Vậy: Khoảng cách từ P đến các cạnh tam giác đều ABC là hằng số.
 Phương pháp II:
Phương pháp II:
Trong tam giác đều ABC, PS
 AC, PR
AC, PR  BC, PQ
BC, PQ  AB và AD
AB và AD  BC. Vẽ PA, PB và PC. Ta có:
BC. Vẽ PA, PB và PC. Ta có:
S(ABC) = S(APB) + S(BPC) + S(CPA).
= ½ AB.PQ + ½ BC.PR + ½ AC.PS
Vì AB = BC = AC
nên S(ABC) = ½ BC (PQ + PR + PS) (1).
Ngoài ra S(ABC) = ½ BC.AD (2).
Từ (1) và (2), ta có: PQ + PR + PS = AD.
Vậy: Khoảng cách từ P đến các cạnh đều ABC là hằng số.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 46
Cho hình thang ABCD. Hai đường chéo cắt nhau tại P. Điểm Q nằm giữa hai đường song song BC và AD sao cho
 AQD =
AQD =  CQB, P và Q ở hai bên CD. Chứng minh
CQB, P và Q ở hai bên CD. Chứng minh BQP =
BQP =  DAQ.
DAQ.
(The diagonals of a trapezoid ABCD intersect at point P. Point Q lies between the parallel lines BC and AD such that
 AQD =
AQD =  CQB, and the line CD separates the points P and Q. Prove that
CQB, and the line CD separates the points P and Q. Prove that  BQP =
BQP =  DAQ).
(G3 (UKR) IMO Shortlist 2007, From the book "The IMO Compendium)
DAQ).
(G3 (UKR) IMO Shortlist 2007, From the book "The IMO Compendium)
BÀI GIẢI
 Từ D vẽ đường thẳng // với QB cắt QP tại R, ta sẽ có các cạnh tỷ lệ bằng nhau:
Từ D vẽ đường thẳng // với QB cắt QP tại R, ta sẽ có các cạnh tỷ lệ bằng nhau: RD/QB = PD/PB = DA/BC
và
 RDA =
RDA =  QBC (cạnh // từng đôi).
QBC (cạnh // từng đôi). Vậy
 RDA ~
RDA ~  QBC
QBC nên:
 ARD =
ARD =  CQB =
CQB =  AQD,
AQD, do đó tứ giác ARQD nội tiếp ==>
 DAQ =
DAQ =  DRQ.
DRQ. Vì
 BQP =
BQP =  DRQ (góc so le trong) suy ra
DRQ (góc so le trong) suy ra  BQP =
BQP =  DAQ.
DAQ.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 47
Vòng tròn nội tiếp với tam giác ABC tiếp xúc các cạnh BC, CA, AB lần lượt tại D, E, F. AD cắt vòng tròn tại X và AX = XD. BX cắt vòng tròn tại Y và CX cắt vòng tròn tại Z. Chứng minh: EY = FZ.
(The incircle of a triangle ABC touches the sides BC, CA, AB at the points D, E, F respectively. Let the line AD intersect this incircle of triangle ABC at a point X (apart from D). Assume that this point X is the midpoint of the segment AD, this means, AX = XD. Let the line BX meet the incircle of triangle ABC at a point Y (apart from X), and let the line CX meet the incircle of triangle ABC at a point Z (apart from X). Show that EY = FZ.
(10th Iberoamerican Olympiad Region V, CHILE. [1995] Problem 5)
BÀI GIẢI
 Hai tam giác CDZ và CXD có
Hai tam giác CDZ và CXD có  XCD chung và
XCD chung và  CDZ =
CDZ =  CXD (chắn cung DZ) nên đồng dạng, cho ta tỷ số: CD / CX = DZ / XD (1)
CXD (chắn cung DZ) nên đồng dạng, cho ta tỷ số: CD / CX = DZ / XD (1)
Tương tự,
 CEZ ~
CEZ ~
 CXE ==> CE / CX = EZ / XE (2)
CXE ==> CE / CX = EZ / XE (2)
Do CD = CE (tính chất tiếp tuyến), ta thấy vế đầu của (1) và (2) bằng nhau, vậy DZ / XD = EZ / XE.
Theo giả thiết AX = XD ==> DZ / AX = EZ / EX,
Ta còn có
 DZE =
DZE =  AXE (chắn cung EXFYD)
AXE (chắn cung EXFYD)
Suy ra
 DZE ~
DZE ~  AXE ==>
AXE ==>  ZED =
ZED =  XEA mà
XEA mà  XEA =
XEA =  EDX (cùng chắn cung EX) nên
EDX (cùng chắn cung EX) nên  ZED =
ZED =  EDX do đó ZE // DX.
EDX do đó ZE // DX.
Chứng minh tương tự, ta cũng có: YF // DX ==> ZE // YF. Do đó, hình thang nội tiếp EFYZ là hình thang cân nên hai đường chéo của chúng bằng nhau. Vậy: EY = FZ
(Lời giải của Đinh Cao Phạn)
T. V. Phê & Nguyễn Tin
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
-
Bài Khảo Cứu & Bài Tập Hình Học (Học Xá) • Bài Khảo Cứu
Cùng Mục (Link) • Có Và Không Của Thế Gian (Hoàng Dung)
• DNA, Đặc Tính Sự Sống và Sinh Vật (Hoàng Dung)
• Thử Tìm Hiểu ChatGPT (Đào Như)
• Những khám phá mới về Chất Trắng Trong Não Bộ (Trần Hồng Văn)
• Siêu Thượng Không Gian: Chương Kết Luận (Trà Nguyễn)
• Vài Mạn Đàm Về Sao Trời (Hoàng Dung)
• Vật Lý Lượng Tử Và Ý Nghĩa Thiền Học Của Vật Chất (Hoàng Dung)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 2) (Trần Hồng Văn)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 1) (Trần Hồng Văn)
• “Mỹ Ngữ” Và “Anh Ngữ” Khác Nhau Thế Nào? (Đàm Trung Pháp)

• Hình Học (Bài Tập)
Bài 48 (Điểm Schiffler của tam giác)
Bài IOM: 7 - 38, 41 - 45, 46 - 51
• Anh Ngữ
• Đố Vui: 1, 2
Liên Kết Trong Mục Học Toán (Học Xá) Liên Kết
IMO
Wolfram MathWorld
The Math Forum
USAmts
Komal
MathLinks
Cut-The-Knot
Từ Điển Anh Việt
|
© Hoc Xá 2002 (T.V. Phê - phevtran@gmail.com) |















