|
|
|
|
|
VĂN HỌC |
GIAI THOẠI | TIỂU LUÂN | THƠ | TRUYỆN | THỜI LUẬN | NHÂN VẬT | ÂM NHẠC | HỘI HỌA | KHOA HỌC | GIẢI TRÍ | TIỂU SỬ |
-
Link Tác Phẩm và Tác Giả Tác Phẩm
Tác Giả
Thơ Văn Trần Y. Hoa & Bằng hữu
Thơ Văn Trần Yên Hoà & Bằng hữu
Tạp Chí
PHONG HÓA & NGÀY NAY
(Đại học Hoa Sen)
TỰ LỰC VĂN ĐOÀN, tác phẩm
(Viện Việt Học)
VĂN HỌC
Tạp chí Văn Học
DÒNG VIỆT
Trọn bộ DÒNG VIỆT
(1993-2009)
VĂN (Xuân Canh Thìn)
(vanmagazine)
TIỂU THUYẾT THỨ BẢY
NAM PHONG - TRI TÂN
THANH NGHỊ - NGÀY NAY
VĂN HOÁ NGÀY NAY
TẬP SAN SỬ ĐỊA
THẾ KỶ 21 - BÁCH KHOA
Tạp Chí VHNT Miền Nam
TÂN VĂN
TIN VĂN
Tạp chí ĐỌC VÀ VIẾT
THƯ QUÁN BẢN THẢO
Sách Xưa
• QUỐC VĂN GIÁO KHOA THƯ:
- Lớp Sơ Đẳng
- Lớp Đồng Ấu
- Lớp Dự Bị
• TỦ SÁCH TIẾNG VIỆT
• KHO SÁCH XƯA
• QUÁN VEN ĐƯỜNG
• LITTLE SAIGON
Phim và Hình Ảnh Xưa
- Cuộc Di Cư Năm 1954
- Phim "Chúng Tôi Muốn Sống"
- Phim "Nắng Chiều", 1973
- Phim Chân Trời Tím, 1971
- Hình ảnh xưa
eBooks
-
Giải Bài Tập Hình Học từ 1 đến 10 (Học Xá) Ad-23-Index Ad-23-Index = (Ad-23-468x60created-2-1-10) (Học Xá)
22-5-2011 | KHOA HỌC
Giải Bài Tập Hình Học từ 1 đến 10
T. V. PHÊ & NGUYỄN TIN
Share File.php Share File




:: Bài 1
Trong hình vuông ABCD chọn một điểm M sao cho MAB là tam giác cân có góc đáy MAB=MBA=15o. Chứng minh MDC là tam giác đều. (GT: AB=BC=CD=DA= a, MA=MB,
 MAB =
MAB =  MBA = 15o, KL:
MBA = 15o, KL:  MDC đều)
MDC đều)
BÀI GIẢI
 a) Phương Pháp Hình Học:
a) Phương Pháp Hình Học:
Chọn một điểm P trên đường trung trực chung của AB và CD (đường thẳng xy), sao cho PAB là một tam giác đều (PA=PB=AB= a). Ta sẽ có
 PAB
= 60o và
PAB
= 60o và  APM=30o
APM=30o
 PAM =
PAM =  PAB +
PAB +  MAB = 60o + 15o = 75o
MAB = 60o + 15o = 75o
 DAM =
DAM =  DAB -
DAB -  MAB = 90o - 15o
= 75o
MAB = 90o - 15o
= 75o
==>
 PAM =
PAM =  DAM (1)
DAM (1)
Hai tam giác PAM và DAM có hai cạnh bằng nhau (cạnh chung AM và AP=AD) kèm giữa một góc bằng nhau (1), vậy chúng bằng nhau. Suy ra:
 ADM =
ADM =  APM = 30o
==>
APM = 30o
==>  MDC = 60o.
MDC = 60o.
Tam giác cân MDC có một góc bằng 60o (
 MDC), nên là tam giác đều.
MDC), nên là tam giác đều.
b) Phương Pháp Lượng Giác:
Áp dụng công thức cộng hàm Lượng giác:
tan(a-b) = (tan a - tan b) / (1+ tan a . tan b) để tính tan15o:
tan15o = tan(60o - 45o) = (tan60o - tan45o) / (1 + tan60o. tan45o) =
(
-1) / (1+
.1) = (
-1).(
-1) / (
+1).(
-1) =
(
-1)2 /
2 -12 = (3+1-2
) / 2 = 2 -
Theo hệ thức lượng trong tam giác vuông MEB, ta có: tan(MBE) = EM / EB
==> EM = tan(MBE) . EB
Vậy EM = tan15o. a/2 = (2-
) . a/2 = a(2-
) / 2
Tương tự, ta có tan(MDF) = MF / FD = (EF - EM) / FD =
[a - a(2 -
)/2] / a/2 = [2a - a(2-
)] / a = (2a-2a+a
) / a =
Vậy
 MDF = 60o ==>
MDF = 60o ==>  MDC đều.
MDC đều.
:: Bài 2
Cho 2 đoạn thẳng bất kỳ bằng nhau: AB = CD. Gọi N là trung điểm của BC và M là trung điểm của AD. Ðường AB cắt MN tại E và cắt CD tại F. Ðường CD cắt MN tại G. Chứng minh tam giác EFG cân tại đỉnh F. (GT: AB = CD, MA = MC, NB = ND, KL: FE = FG)
BÀI GIẢI
 Vẽ thêm 2 hình bình hành ABNK và DCNL.
Vẽ thêm 2 hình bình hành ABNK và DCNL.
Ta có: AK = DL (= BN = CN)
AK // DL (// BC)
Tứ giác AKDL có hai cạnh đối diện AK & DL vừa song song vừa bằng nhau, vậy là hình bình hành. Do đó hai đường chéo AD & KL của chúng phải cắt nhau tại trung điểm M.
Tam giác KNL cân (NK = NL = AB = CD) nên đường trung tuyến NM cũng là đường phân giác.
Suy ra:
 N1 =
N1 =  N2 (1)
N2 (1)
Ta có:
 N1 =
N1 =  E1 (góc đồng vị)
E1 (góc đồng vị)
 N2 =
N2 =  G (góc đồng vị)
G (góc đồng vị)
Từ (1) ==>
 E1 =
E1 =  G Vì
G Vì  E1 =
E1 =  E2 (góc đối đỉnh) ==>
E2 (góc đối đỉnh) ==>  E2 =
E2 =  G
G
Vậy tam giác EFG cân.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 3
Cho hình bình hành ABCD và bên trong là hình bình hành A'B'C'D'. M, N, P, Q theo thứ tự là trung điểm của các cạnh AA', BB', CC', DD'. Chứng minh MNPQ cũng là một hình bình hành.
BÀI GIẢI
 Kẻ thêm 2 đường thẳng AB' và CD'. Gọi M', P' lần lượt là trung điểm của AB' và CD'.
Kẻ thêm 2 đường thẳng AB' và CD'. Gọi M', P' lần lượt là trung điểm của AB' và CD'.
Ta có: MM' // = 1/2 A'B' (*)
PP' // = 1/2 D'C' .
Vì A'B' = D'C' (cạnh của hình bình hành A'B'C' D') nên MM' //= PP'.
Vậy tứ giác MM'PP' là hình bình hành, hai đường chéo MP, M'P' của chúng phải cắt nhau tại trung điểm (1).
Tương tự như trên, ta có:
M'N // = 1/2 AB
P'Q // = 1/2 CD .
Vì AB = CD (cạnh của hình bình hành ABCD) nên M'N // = P'Q.
Vậy tứ giác M'NP'Q là hình bình hành, hai đường chéo M'P', NQ của chúng phải cắt nhau tại trung điểm (2).
Từ (1) và (2) suy ra I là trung điểm chung cuả 3 đoạn thẳng MP, M'P', NQ.
Tứ giác MNPQ có hai đường chéo MP và NQ giao nhau tại trung điểm nên là một hình bình hành.
(*) Xin xem Ðịnh lý 8 trong phần Các Ðịnh Lý về Hình Bình Hành
:: Bài 4
Cho tam giác đều ABC. Ðường AQ bất kỳ (điểm Q nằm trên BC) cắt vòng tròn ngoại tiếp tại P. Chứng minh: 1 / PB + 1 / PC = 1 / PQ
BÀI GIẢI
 Kéo dài CP một đoạn PN = PB. Tam giác cân BPN có BPN = 60o (chắn cung BC) nên cũng là tam giác đều. Suy ra PQ // NB và PQC đồng dạng với NBC. Ta có hệ thức đồng dạng: PQ / NB = PC / NC (1)
Kéo dài CP một đoạn PN = PB. Tam giác cân BPN có BPN = 60o (chắn cung BC) nên cũng là tam giác đều. Suy ra PQ // NB và PQC đồng dạng với NBC. Ta có hệ thức đồng dạng: PQ / NB = PC / NC (1)
Vì NB = PB ( BPN đều) và NC = NP + PC = PB + PC, nên hệ thức (1) trở thành:
PQ / PB = PC / (PB+PC)
PQ (PB + PC) = PB . PC
PQ . PC + PQ . PB = PB . PC (2)
Chia 2 vế của hệ thức (2) cho PB . PC . PQ, ta được:
1 / PB + 1 / PC = 1 / PQ
:: Bài 5
Cho hai vòng tròn cắt nhau tại B và D và một cát tuyến ABC bất kỳ. Gọi:
M là trung điểm đoạn AC.
K là trung điểm cung AD
N là trung điểm cung CD (cung AD & CD nằm về phía không chứa điểm B).
Chứng Minh: KM thẳng góc với NM.
BÀI GIẢI
 Kéo dài KM một đoạn ML = MK, đoạn NM sẽ là trung tuyến của tam giác KNL. Nếu ta chứng minh được tam giác KNL cân thì trung tuyến NM cũng chính là đường cao của tam giác này. Và như thế KM sẽ thẳng góc với NM.
Kéo dài KM một đoạn ML = MK, đoạn NM sẽ là trung tuyến của tam giác KNL. Nếu ta chứng minh được tam giác KNL cân thì trung tuyến NM cũng chính là đường cao của tam giác này. Và như thế KM sẽ thẳng góc với NM.
Thật vậy, vì M là trung điểm của hai đường chéo AC và KL nên tứ giác AKCL là hình bình hành.
Suy ra:
LC // KA ==>
 xAB=
xAB= LCy (góc đồng vị),
LCy (góc đồng vị),
LC = KA ==> LC = KD (1)
Theo giả thiết: N là trung điểm cung CD nên: NC=ND (2)
Xét hai góc KDN và LCN,
 KDN =
KDN =  BDN+
BDN+ KDB, vì
KDB, vì  BDN=
BDN= yCN (cùng chắn cung BN) và
yCN (cùng chắn cung BN) và  KDB =
KDB =  xAB (cùng chắn cung BK) =
xAB (cùng chắn cung BK) =  LCy
LCy
Vậy KDN = yCN + LCy = LCN (3)
Hai tam giác KDN và LCN có hai cạnh bằng nhau (1&2), kèm giữa một góc bằng nhau (3). Vậy chúng bằng nhau. Suy ra KN = LN ==> tam giác KNL cân.
Do đó: KM
 NM
NM
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 6
Cho tam giác cân ABC: A = 20o, AD = BC. Tính DCA?
 BÀI GIẢI
BÀI GIẢI
Vẽ thêm tam giác cân AED với góc ở đỉnh E = 20o, ta sẽ có:
 ADE =
ADE =  DAE = (180o - 20o) / 2 = 80o.
DAE = (180o - 20o) / 2 = 80o.
Vậy
 CAE =
CAE =  DAE -
DAE -  DAC = 80o - 20o
= 60o
DAC = 80o - 20o
= 60o ==> CAE là tam giác đều.
Suy ra:
 AEC = 60o ==>
AEC = 60o ==>  DEC = 40o,
DEC = 40o,
EC = EA = ED ==>
 DEC cân,
DEC cân,
vậy
 DCE =
DCE =  CDE = (180o- 40o)/2 =70o.
CDE = (180o- 40o)/2 =70o.
 DCA =
DCA =  DCE -
DCE -  ACE = 70o - 60o,
ACE = 70o - 60o, ==>
 DCA = 10o
DCA = 10o
 Cách Giải Khác:
Cách Giải Khác:
Vẽ thêm tam giác đều AED.
Xét hai tam giác EAC và BCA, chúng có:
 EAC =
EAC =  BCA (= 80o)
BCA (= 80o)
EA = BC
cạnh AC chung,
nên chúng bằng nhau, suy ra CE = AB = CA ==>
 ECA cân.
ECA cân.
Vậy CD chính là đường phân giác của ECA, ==>
 DCA = 10o
DCA = 10o
:: Bài 7
Cho hình bình hành ABCD. Từ D và B, kẻ hai đường thẳng tạo với DC và BC hai góc bằng nhau (
 PDC =
PDC =  PBC). Chứng minh
PBC). Chứng minh  DPA =
DPA =  BPC.
BPC.
 BÀI GIẢI
BÀI GIẢI
Vẽ thêm hình bình hành BQPC, ta sẽ có:
1)
 = PBC (góc so le trong) (1)
= PBC (góc so le trong) (1)
2) QP //= BC //= AD nên AQPD cũng là hình bình hành ==> AQ // DP,
suy ra
 QAB =
QAB =  PDC =
PDC =  PBC (2)
PBC (2) Từ (1) và (2) ta có:
 =
=  QAB, vậy tứ giác ABQP nội tiếp trong một vòng tròn. Do đó:
QAB, vậy tứ giác ABQP nội tiếp trong một vòng tròn. Do đó: +
+
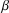 =
=  AQB (chắn cung AB)
AQB (chắn cung AB) +
+
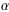 =
=  DPC =
DPC =  AQB (góc có 2 cặp cạnh song song)
AQB (góc có 2 cặp cạnh song song)
==>
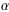 =
=
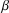 ==>
==>  DPA =
DPA =  BPC
BPC
:: Bài 8
Cho tam giác cân ABC có góc ở đỉnh A = 20o. Vẽ những đường thẳng bên trong tam giác tạo thành các góc sau:
 DBC = 60o ,
DBC = 60o ,  ECB = 50o . Tính góc EDB ?
ECB = 50o . Tính góc EDB ?
BÀI GIẢI
 Trong tam giác ABC, vẽ đường thẳng BF = BC. Ta sẽ có:
Trong tam giác ABC, vẽ đường thẳng BF = BC. Ta sẽ có:
 FBC = 20o,
FBC = 20o,  FBE = 60o,
FBE = 60o,  BEC = 50o.
BEC = 50o.
Vậy
 EBC cân ==> EB = BC = BF ===>
EBC cân ==> EB = BC = BF ===>
 EBF cân.
EBF cân.
Tam giác cân EBF có một góc bằng 60o (
 FBE), nên là tam giác đều
FBE), nên là tam giác đều
==> BF = FE (1).
 BFD có
BFD có  FBD =
FBD =  FDB = 40o nên là tam giác cân
FDB = 40o nên là tam giác cân==> BF = FD (2).
Từ (1) và (2) ta có
 EFD cũng cân. Tam giác này có góc ở đỉnh là:
EFD cũng cân. Tam giác này có góc ở đỉnh là:  EFD = 180o - (
EFD = 180o - ( EFB +
EFB +  BFC) = 180o - (60o + 80o) = 40o
BFC) = 180o - (60o + 80o) = 40o Vậy góc đáy EDF của chúng = 70o, suy ra
 EDB = 30o.
EDB = 30o.
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
:: Bài 9
I là trung điểm dây cung AB của vòng tròn (O). Qua I, vẽ hai dây cung bất kỳ CD và EF. CF và ED cắt AB tại M và N. Chứng Minh: IM = IN.
BÀI GIẢI
 Hai tam giác FIC và DIE đồng dạng vì có hai góc bằng nhau từng đôi một (
Hai tam giác FIC và DIE đồng dạng vì có hai góc bằng nhau từng đôi một ( F =
F =  D,
D,  C =
C =  E). Ta được tỷ lệ thức:
E). Ta được tỷ lệ thức:
FI/DI = FC/DE (1)
Kẻ hai đường trung tuyến IK và IL, xét hai tam giác FIK và DIL, chúng có:
 F =
F =  D
D
Từ (1) và từ tính chất đường trung tuyến ta cũng có:
FI /DI = 2FK/2DL = FK/DL
Vậy chúng đồng dạng, suy ra:
 K1 =
K1 =  L1 (2)
L1 (2)
Nối tâm O đến trung điểm các dây cung AB, FC, DE, ta có:
OI
 AB, OK
AB, OK  FC, OL
FC, OL  DE.
DE.
Suy ra hai tứ giác OIMK và OINL nội tiếp trong hai vòng tròn. Vậy:
 K1 =
K1 =  O1 (cùng chắn cung IM của vòng ngoại tiếp tứ giác OIMK)
O1 (cùng chắn cung IM của vòng ngoại tiếp tứ giác OIMK)
 L1 =
L1 =  O2 (cùng chắn cung IN của vòng ngoại tiếp tứ giác OINL)
O2 (cùng chắn cung IN của vòng ngoại tiếp tứ giác OINL)
So sánh với (2) ta được
 O1 =
O1 =  O2, nên OI cũng chính là đường phân giác của
O2, nên OI cũng chính là đường phân giác của
 MON.
MON.
Trong
 MON, OI vừa là đường cao, vừa là đường phân giác, vậy OI cũng là đường trung tuyến, do đó: IM = IN.
MON, OI vừa là đường cao, vừa là đường phân giác, vậy OI cũng là đường trung tuyến, do đó: IM = IN.
:: Bài 10
I là trung điểm dây cung AB của vòng tròn (O). Qua I, vẽ hai dây cung bất kỳ CD và EF. EC và FD cắt AB tại M và N. Chứng Minh: IM = IN.
BÀI GIẢI
 1) Phương Pháp Hình Học:
1) Phương Pháp Hình Học:
Tương tự như bài kỳ trước ta có hai tam giác FID & CIE đồng dạng ==>
 FIK ~
FIK ~ CIL
CIL
==>
 FKI =
FKI =  MLI.
MLI.
Cũng từ hai tứ giác OIKN & OIML nội tiếp trong hai vòng tròn nên ta có:
 FKI =
FKI =  ION,
ION,  MLI =
MLI =  IOM. Suy ra:
IOM. Suy ra:  IOM =
IOM =  ION.
ION.
Do đó: IM = IN
2) Phương Pháp Ðại Số:
 Ðặt IA = IB = a, IM = y, IN = x, MQ = y1, MP = y2, NS = x1, NR = x2.
Ðặt IA = IB = a, IM = y, IN = x, MQ = y1, MP = y2, NS = x1, NR = x2.
Hai tam giác vuông NSF và MPC có
 F =
F =  C nên đồng dạng, ta có:
C nên đồng dạng, ta có:
NS/MP = NF/MC ==> x1 / y2 = NF/MC
Hai tam giác vuông NRD và MQE có
 D =
D =  E nên đồng dạng, ta có:
E nên đồng dạng, ta có:
NR/MQ = ND/ME ==> x2 / y1 = ND/ME Vậy: (x1.x2)/(y1.y2)=(NF.ND)/(MC.ME) (1)
Ta cũng có:
 NSI ~
NSI ~  MQI
MQI
==> NS/MQ = NI/MI ==> x1 / y1 = x / y
 NRI ~
NRI ~  MPI
MPI
==> NR/MP = NI/MI ==> x2 / y2 = x / y
Vậy: (x1.x2) / (y1.y2) = x2 / y2 (2)
Từ (1&2) suy ra: x2/y2 = (NF.ND)/(MC.ME) = (NA.NB)/(MA.MB)
= [(x+a).(x-a)] / [(y-a).(y+a)] = (x2-a2)/(y2-a2)
==> x2(y2 - a2) = y2 (x2 - a2)
==> x2y2 - x2a2 = y2x2 - y2 a2
==> x2 = y2
==> x = y Do đó: IM = IN
T. V. Phê & Nguyễn Tin
Ad-22-A_Newest-Feb25-2022 Ad-22-A_Newest-Feb25-2022
-
Bài Khảo Cứu & Bài Tập Hình Học (Học Xá) • Bài Khảo Cứu
Cùng Mục (Link) • Có Và Không Của Thế Gian (Hoàng Dung)
• DNA, Đặc Tính Sự Sống và Sinh Vật (Hoàng Dung)
• Thử Tìm Hiểu ChatGPT (Đào Như)
• Những khám phá mới về Chất Trắng Trong Não Bộ (Trần Hồng Văn)
• Siêu Thượng Không Gian: Chương Kết Luận (Trà Nguyễn)
• Vài Mạn Đàm Về Sao Trời (Hoàng Dung)
• Vật Lý Lượng Tử Và Ý Nghĩa Thiền Học Của Vật Chất (Hoàng Dung)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 2) (Trần Hồng Văn)
• Những Quan Niệm và Học Thuyết Mới về Vũ Trụ (Phần 1) (Trần Hồng Văn)
• “Mỹ Ngữ” Và “Anh Ngữ” Khác Nhau Thế Nào? (Đàm Trung Pháp)

• Hình Học (Bài Tập)
Bài 48 (Điểm Schiffler của tam giác)
Bài IOM: 7 - 38, 41 - 45, 46 - 51
• Anh Ngữ
• Đố Vui: 1, 2
Liên Kết Trong Mục Học Toán (Học Xá) Liên Kết
IMO
Wolfram MathWorld
The Math Forum
USAmts
Komal
MathLinks
Cut-The-Knot
Từ Điển Anh Việt
|
© Hoc Xá 2002 (T.V. Phê - phevtran@gmail.com) |

















